Donner du sens à un calcul

L’interface propose des associations d’icônes et d’images faisant référence à notre quotidien permettant ainsi de donner du sens au calcul demandé a contrario des questions du type « opérande opérateur opérande » par ailleurs indispensables, où l’écriture chiffrée fait perdre au calcul son caractère concret. Cependant, loin d’être opposées, ces deux activités (représentation visuelle et représentation chiffrée) restent complémentaires, l’expérience montrant que l’étape visuelle s’avère même indispensable pour certains élèves qui éprouvent des difficultés à passer à l’étape d’abstraction.

Si l’approche visuelle permet de donner au calcul du sens qualitatif comme on vient de le voir, elle permet aussi de développer le sens de la quantité. Prenons à titre d’exemple l’élève qui au cours d’un exercice de calcul mental chiffré affirme que « 9 x 7 = 23 » ; dans ce cadre, l’automatisation l’emporte sur la notion de quantité et l’aberrance de l’erreur produite n’est pas perçue par l’élève.  L’aspect quantitatif a été occulté par l’automatisation combinée à une mauvaise mémorisation. Si ce même élève est face au même calcul proposé cette fois par le dessin d’un calendrier comportant neuf semaines (exemple ci-dessous ), l’image fait prendre conscience à l’élève de l’ordre de grandeur du résultat attendu et de l’aberrance de sa proposition :

Servir de point d’appui pour

la mémorisation

Certains élèves ne parviennent pas à mémoriser de façon satisfaisante les tables de multiplication malgré un entraînement répété ; une représentation mentale des nombres combinée à la compréhension des opérations en jeu est alors nécessaire. L’interface de HowMany intègre un support qui permet à l’élève de construire du lien entre les représentations imagées du nombre et les représentations liées aux codages issus des systèmes de numération, chiffrée ou verbale, favorisant ainsi le processus de mémorisation.

Analysons le comportement de l’élève face à l’exemple qui suit :

– Première étape : Visualisation et compréhension du  « 9 x 4 »

Etape, qui suivant la complexité du dessin, peut s’avérer plus ou moins longue.

– Deuxième étape : combien font  9 x 4 ?

C’est précisément dans cette phase que le calcul automatisé intervient, et c’est aussi là que le joueur fait appel à sa mémoire. Dans le cas où il ne donne pas le résultat attendu, l’application le corrige :

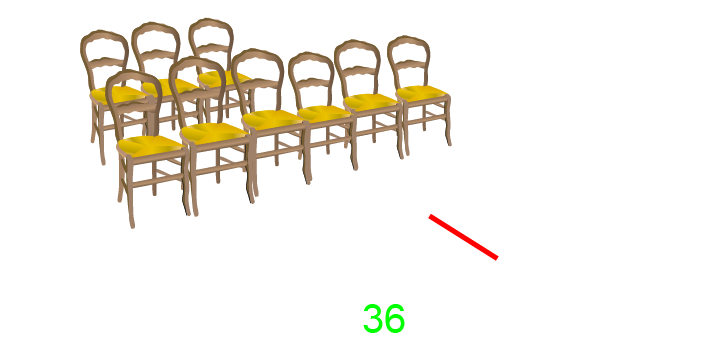
La formule de correction proposée par l’interface est essentielle car elle construit du lien entre les deux représentations (imagées et chiffrées) et favorise du même coup le processus de mémorisation.

L’interface favorise le mécanisme de va-et-vient entre les deux représentations qui permet la mémorisation des tables : dans l’erreur, c’est la représentation imagée qui vole au secours de la représentation abstraite chiffrée, tandis que dans le cas de la réussite, c’est la représentation chiffrée acquise qui a permis au joueur de « résoudre » la représentation imagée. Ce qui permet l’automatisation des calculs simples via la reproduction de résultats immédiatement disponibles et la récupération en mémoire ou reconstruction instantanée.

Développer l’aptitude à associer la bonne opération à un problème donné

Si le graphisme de chaque dessin joue un rôle essentiel pour rendre l’application attractive, l’objectif principal de l’image est avant tout de signifier un calcul lié à une ou plusieurs opérations. C’est précisément dans ce but quel les images ont été initialement conçues : donner du sens aux opérations via une représentation imagée, ce qui permet en particulier au joueur de développer sa capacité à associer la bonne opération à une situation donnée.

        L’origine de la difficulté de l’élève à associer la bonne opération à un problème élémentaire donné fait l’objet de nombreux débats. Une hypothèse récurrente explique que cela pourrait provenir d’un manque d’expérience dans l’analyse, l’observation et la compréhension de situations de la vie quotidienne faisant intervenir l’une des quatre opérations élémentaires (raisons qui peuvent être d’ordre culturel, ou liées au développement intellectuel de l’enfant). Revenir sur cette aptitude le plus tôt possible, la travailler régulièrement est primordial dans la mesure où est elle est nécessaire à une bonne appréhension de certaines notions mathématiques abordées par la suite.

          De nombreux réflexes pédagogiques (comme celui qui consiste à illustrer un problème donné par un schéma ) permettent de revenir naturellement sur ces aptitudes. Néanmoins, l’expérience montre que ces pratiques doivent être fréquentes et construites à partir de beaucoup d’exemples pour espérer ancrer des mécanismes durables dans le temps. La présentation de Howmany sous forme de jeu sur tablette semble être une réponse satisfaisante à ce besoin quantitatif : en effet, le logiciel permet à l’élève de revenir seul, par épisodes plus ou moins longs sur des jeux proposant chacun plusieurs dizaines de configurations différentes. C’est en jouant que les réflexes vont se construire et que l’aptitude se développera de façon pérenne.

Du calcul automatisé au calcul réfléchi

Mettre en place des automatismes liés à la proportionnalité

La répétition d’objets identiques, principe de base sur lequel le jeu s’appuie est implicitement lié à la proportionnalité ; l’élève est parfois amené à bâtir des raisonnements du type : puisque n objets contiennent p éléments alors k x n objets en contiendront k x p. La nature des dessins et l’évolution progressive du jeu permettent alors de bien distinguer ce qu’il faut mémoriser ou automatiser ( les tables, quelques doubles et moitiés, …) de ce qu’il faut être capable de reconstruire ( et qui relève du calcul réfléchi) ; ainsi le travail sur la proportionnalité s’effectue à plusieurs niveaux.

Eradiquer les stratégies parallèles

Indispensable pour rythmer une partie de jeu, le timing évolue en fonction du niveau du joueur et d’un certain nombre de paramètres (progression, vitesse de réponse du joueur, bonus et malus, points de vie restants… ). Le timing favorise par ailleurs le calcul automatisé et en particulier l’assimilation des tables de multiplication, il empêche le joueur d’avoir recours à des stratégies parallèles comme « le comptage sur les doigts ».

Observons sur cet exemple la réaction de cet élève qui pense à voix haute, nous révélant ainsi sa démarche : «  2,4,6,8,10,12… et donc ça fait 14 ! »

Compter de deux en deux lui a permis d’éviter d’avoir recours à la multiplication directe ; stratégie parallèle qui au premier abord semble porter préjudice au principe du jeu. Bien au contraire, il suffit de le confronter à d’autres élèves ou bien tout simplement d’utiliser un timing pour que l’élève s’aperçoive que de compter de cette manière lui fait perdre un temps précieux. Il prend alors conscience de la nécessité de connaître ses tables. En outre, les tableaux proposés par HowMany étant de plus en plus chargés à mesure que le niveau augmente, les stratégies parallèles de ce type deviennent inutilisables montrant une fois de plus au joueur l’intérêt de maîtriser ses tables pour obtenir rapidement les résultats attendus.

Le ludique au service de la motivation

Il est admis depuis plusieurs années que le jeu constitue la première source d’engagement et de motivation parmi les apprenants en formation que ce soit sous forme présentielle (comme les jeux de rôles ou les jeux-cadres d’entreprise) ou en ligne (comme les Serious Games). Plusieurs expérimentations menées dans mes classes autour de différents jeux dédiés au calcul mental dans des contextes variés m’ont permis d’observer une nette préférence des élèves pour ce que j’allais baptiser « HowMany ». La raison de ce succès ne se résume donc pas à la seule dimension ludique même si celle-ci est indispensable. La force de HowMany réside dans l’alliage entre le visuel et le ludique ; un alliage qui rend indéniablement l’application attractive et qui trouve naturellement sa place dans une société où l’accès au savoir se fait de plus en plus par l’image.

      La grande force de HowMany résidant dans le fait que tout cet aspect pédagogique demeure totalement invisible aux yeux du joueur focalisé sur la dimension ludique. C’est ainsi que durant mes années d’enseignement, j’ai pu observer beaucoup d’élèves devenir littéralement accrocs au principe du jeu.